ａ、ｂを正の数とし、ｘｙ平面の２点Ａ（ａ，０）およびＢ（０，ｂ）を
頂点とする正３角形をＡＢＣとする。
ただし、Ｃは第１象限の点とする。
(1)３角形ＡＢＣが正方形Ｄ＝｛（ｘ，ｙ）｜０≦ｘ≦１，０≦ｙ≦１｝
　に含まれるような（ａ，ｂ）の範囲を求めよ。
(2)（ａ，ｂ）が(1)の範囲を動くとき、３角形ＡＢＣの面積Ｓが最大と
　なるような（ａ，ｂ）を求めよ。
　また、そのときのＳの値を求めよ。

（解）
(1)
　 → → →
　　ＯＣ＝ＯＢ＋（ＢＡの６０゜回転） だから
　複素数平面上でＡに対応する点が、ａ
                        Ｂ　　〃　　　　      　ｂｉ
                        Ｃ    〃　　    　は、
　　ｂｉ＋(ａ−ｂｉ)(cos６０゜＋ｉsin６０゜)

       １       �浮R       �浮R       １
　＝---ａ＋----ｂ＋(----ａ＋----ｂ)ｉ
       ２        ２          ２         ２

　よって、３角形がＤに含まれるための条件は、３頂点がＤに含まれる
　ことであり、
　　ａ＞０、ｂ＞０（条件）、ａ≦１、ｂ≦１
      １       �浮R       　　�浮R       １
　　---ａ＋----ｂ≦１、 ----ａ＋----ｂ≦１ 
      ２        ２         　　 ２         ２
   つまり、
                  １          ２
        ｂ≦−----ａ＋----    と、   ｂ≦−√３ａ＋２    が成り立つときである。
                √３       √３

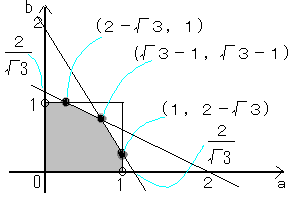
　ゆえに、求める（ａ，ｂ）の範囲は、下図の部分である。

(2)
         �浮R          �浮R
　Ｓ＝----ＡＢ^２＝----(ａ^２＋ｂ^２)
          ４             ４
　ここで、ａ^２＋ｂ^２は、Ｏと(ａ，ｂ)との距離の２乗であるから、
　Ｓを最大にする(ａ，ｂ)は上図の３つの丸のうちのどれかである。
実際に求めてみると、(２−�浮R)^２＋１^２＝８−４�浮R
　　　　　　　　　　　(�浮R−１)^２＋(�浮R−１)^２＝８−４�浮R
　だから、３つともＳを最大にする。
　よって求める(ａ，ｂ)は３つあって、
　　(２−�浮R，１)，(�浮R−１，�浮R−１)，(１，２−�浮R)
　であり、最大のＳは�浮R(２−�浮R)＝２�浮R−３