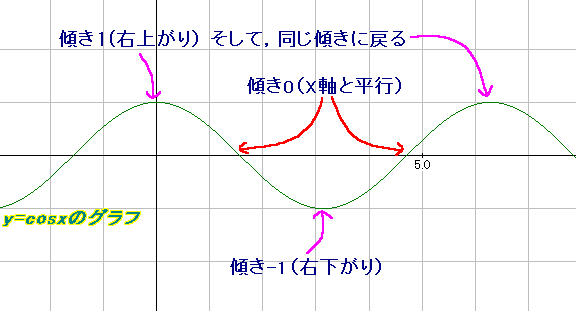
پ@(sinX)'=cosX
‚ً•\‚·پB

| ژOٹp”ن‚ج”÷•ھŒِژ®
پ@(sinX)'=cosX ‚ً•\‚·پB |
 |
 |
”÷•ھ‚ج’è‹`‚و‚èپC
پ@پ@پ@پ@پ@پ@پ@پ@پ@sin(X+ƒ¢Xپjپ|sinX
پisinXپjپfپپlim------------------
پ@پ@پ@پ@ پ@ƒ¢Xپ¨0پ@پ@پ@ƒ¢X
•ھژq‚ة‰ء–@’è—‚ًژg‚¤‚ئپC
پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@sinXcosƒ¢Xپ{cosXsinƒ¢Xپ|sinX
پ@پ@پ@پ@پ@پپlim----------------------------پ@پ@
پ@پ@پ@پ@پ@پ@ƒ¢Xپ¨0پ@پ@پ@پ@پ@پ@
ĢX
•ھژq‚ًگ®—‚µ‚ؤپC
پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@sinX(cosƒ¢Xپ|1)پ{cosXsinƒ¢X
پ@پ@پ@پ@پ@پپlim----------------------------پ@پ@
پ@پ@پ@پ@پ@پ@ƒ¢Xپ¨0پ@پ@پ@پ@پ@پ@پ@ƒ¢X
چX‚ةپC‹ةŒہ‚ً‚Q‚آ‚ة•ھٹ„‚µ‚ؤچl‚¦‚é‚ئپC
پ@پ@ پ@پ@پ@پ@پ@پ@پ@پ@
پ@پ@cosƒ¢Xپ|1پ@پ@پ@پ@ پ@پ@پ@ پ@ پ@ sinƒ¢X
پ@پ@پ@پ@پ@پپsinX پ~ lim-----------پ@پ{پ@cosX
پ~ lim----------پ@پ@پcپcپcپcپ¦
پ@پ@پ@پ@ پ@پ@پ@پ@
پ@ƒ¢Xپ¨0پ@ ƒ¢Xپ@پ@پ@پ@پ@
پ@پ@ ƒ¢Xپ¨0پ@ ƒ¢Xپ@
‚ئ‚ب‚éپB
پ@
چإڈ‰‚ةپCپ¦ژ®‚ج‰E”¼•ھ‚ج‹ةŒہ‚ًچl‚¦‚éپB
ƒ¢Xپپh‚ئ‚¨‚¢‚ؤپC
پ@ پ@پ@پ@پ@پ@پ@پ@پ@ sinƒ¢Xپ@پ@پ@پ@
پ@ پ@پ@پ@sinh
پ@پ@پ@پ@پ@پ@پ@lim----------پ@=پ@پ@lim--------پ@‚ًژ¦‚·پB
پ@پ@پ@پ@پ@پ@ƒ¢Xپ¨0پ@
ƒ¢Xپ@پ@پ@ پ@hپ¨0پ@
پ@ hپ@پ@
پ@
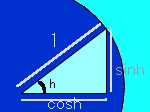
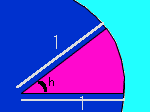
’Pˆت‰~‚ة‚¨‚¢‚ؤپC‰؛گ}‚ج‚و‚¤‚بژOٹpŒ`ْ@‚ئگîŒ`ْA‚ئژOٹpŒ`ْB‚ج–تگد‚ًچl‚¦‚éپB
| ْ@ | ْA | ْB | “®‚گ} | |
 |
 |
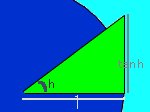 |
‚±‚ê‚ح |  |
‚ھگ¬‚è—§‚آپB‘S‘ج‚ةپ@2/sinh‚ً‚©‚¯‚é‚ئپC
پ@ پ@
پ@پ@پ@پ@hپ@پ@ پ@پ@1
coshپƒ--------پƒ--------
پ@پ@
پ@پ@پ@sinhپ@ پ@پ@cosh
چX‚ةپC‹tگ”‚ًژو‚é‚ئ•s“™چ†‚جŒü‚«‚ھ‹t“]‚µپC
پ@پ@1پ@پ@پ@پ@
sinh
--------پ„---------پ„cosh
پ@coshپ@پ@پ@
پ@h
‹ةŒہ‚ًژو‚é‚ئپC
پ@پ@پ@پ@1پ@پ@پ@پ@
پ@sinh
lim--------پ„lim---------پ„lim
cosh
hپ¨0پ@coshپ@
پ@hپ¨0پ@ hپ@ پ@
پ@hپ¨0
پ@
‚±‚جژ®‚ة‚¨‚¢‚ؤپCچ¶‚جچ€‚ئ‰E‚جچ€‚ة‚آ‚¢‚ؤپC
پ@ پ@پ@پ@1پ@پ@پ@پ@پ@
limپ@--------پ@پپپ@lim
coshپ@پپپ@1پ@‚¾‚©‚çپC
hپ¨پ}0پ@ coshپ@پ@
پ@hپ¨پ}0
پiپ}0‚ئ‚حپCگ³‚ج•û‚©‚ç0‚ة‹ك‚أ‚¯‚邱‚ئ‚ئپC•‰‚ج•û‚©‚ç0‚ة‹ك‚أ‚¯‚邱‚ئ‚ًˆس–،‚µ‚ؤ‚¢‚éپBپj
‚و‚ء‚ؤ‚ح‚³‚ـ‚ꂽپC’†‰›‚جچ€‚ج‹ةŒہ’lپC
پi‹²‚فŒ‚‚؟ƒپƒ\ƒbƒhپj
پ@ پ@پ@sinh
lim---------پ@پپپ@1پ@‚ئ‚ب‚éپB
hپ¨0پ@پ@
hپ@پ@
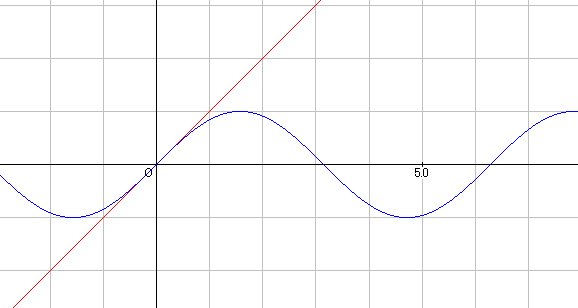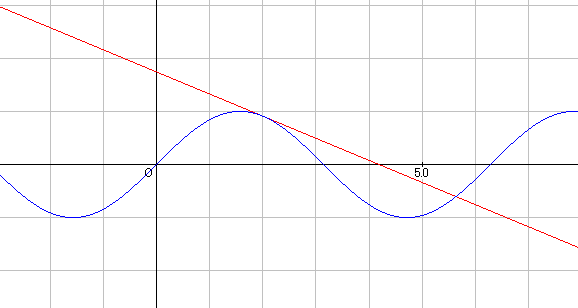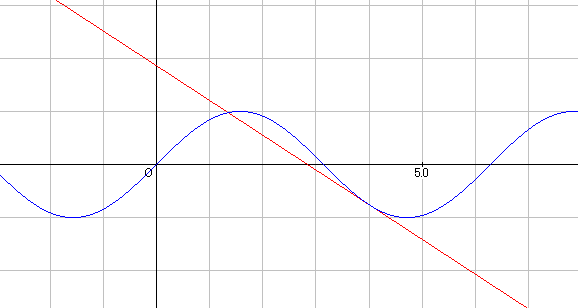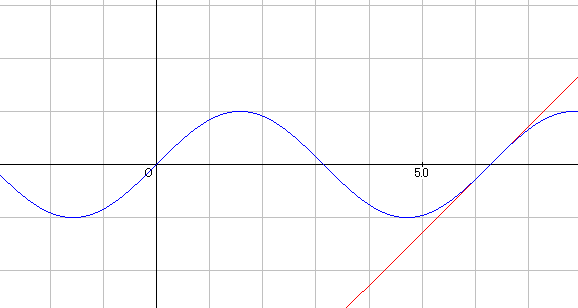
‚±‚ê‚حپCŒ´“_‚ة‚¨‚¯‚ésinX‚جŒX‚«‚ھ‚P‚ئ‚ب‚邱‚ئ‚ًژ¦‚µ‚ؤ‚¢‚éپB
پ@
ژں‚ةپCپ¦ژ®‚جچ¶”¼•ھ‚ج‹ةŒہ‚ًچl‚¦‚éپB
ƒ¢Xپپh‚ئ‚¨‚¢‚ؤپC
پ@ پ@پ@ پ@cosƒ¢Xپ|1پ@پ@پ@پ@
پ@پ@پ@پ@coshپ|1پ@
پ@پ@پ@lim--------------پ@پپپ@lim----------
‚ًژ¦‚·پB
پ@پ@ƒ¢Xپ¨0پ@
ƒ¢Xپ@پ@پ@پ@ پ@پ@hپ¨0پ@پ@
h
•ھ•ê•ھژq‚ة(coshپ{1)‚ً‚©‚¯‚ؤپC
پ@
پ@ پ@پ@coshپ|1پ@پ@پ@پ@پ@
پ@پ@(cosh-1)(cosh+1)
lim------------پ@پپپ@lim------------------
hپ¨0پ@ پ@ پ@hپ@پ@پ@
پ@ پ@پ@hپ¨0پ@پ@ h(cosh+1)
پ@پ@ پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
پ@cos2h-1
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپپ@lim-------------پ@پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@hپ¨0پ@پ@
h(cosh+1)
پ@
پ@ پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ|sin2h
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپپ@lim-------------پ@پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@hپ¨0پ@
h(cosh+1)
پ@پ@ پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@sinhپ@
پ@پ@پ@ پ@1
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپپ@پ|پilimپ@sinhپj(lim------)(lim----------)پ@پ@
پ@ پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@hپ¨0پ@پ@پ@
پ@hپ¨0پ@پ@hپ@پ@hپ¨0پ@
cosh+1
پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@1
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپپ@پ|1پ~پ@(
0 )پ@پ~پ@( ‚P )پ@پ~پ@-------
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
( 1 + 1 )
پ@پ@پ@پ@پ@پ@پ@پ@پ@پپپ@
0
‚ً“¾‚éپB
‚و‚ء‚ؤپCچإڈ‰‚جپ¦ژ®‚ح
پ@پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@ cosƒ¢Xپ|1پ@پ@پ@پ@ پ@
پ@پ@پ@ پ@sinƒ¢X
پ@پ@(sinX)پfپپsinX پ~
lim-----------پ@پ{پ@cosX پ~ lim----------
پ@پ@پ@پ@پ@پ@پ@پ@پ@
پ@پ@ƒ¢Xپ¨0پ@ ƒ¢Xپ@پ@پ@پ@پ@پ@
پ@ پ@پ@ƒ¢Xپ¨0پ@ ƒ¢Xپ@
پ@
پ@پ@پ@پ@پ@پ@پپپ@sinXپ@پ~پ@0پ@پ{پ@cosXپ@پ~پ@1
پ@پ@پ@پ@پ@پ@پپپ@cosX
‚ئ‚ب‚éپB