![]() �~���̎ߐؒf�ŕ����邱��
�~���̎ߐؒf�ŕ����邱��
�`�̐ρC�f�ʂ̕`���Ȑ��C���ʐςɂ��ā`
���������������w�Z
�@�@���@�@�����K�v
http://www.synapse.ne.jp/dozono/
�@
|
�P�@�͂��߂� �@�������O�ɂȂ邪�C���̓���E�l�b�g�ŁC���]�̂̋��ϖ��Ɋւ��āC���A�X�`���[����ؒf�������p�Q���ӎO�p�`��ςݏd�˂�`�ł̎����f�����쐬����Ƃ������|�[�g���o�����Ă����������B���̖��̎��ӂ��l���Ă������C����������E�l�b�g�ŎR�������⍑�����w�Z�̐����搶�́C�u�Ώ̐��̂�����̒�ϕ��̒l�ɂ��āv�Ƃ������|�[�g��ǂނƁC���̃C���[�W���Ă������̂Ǝ������̂����������߁C���̂悤�Ȍ��e���쐬����Ɏ������B�~���̎ߐؒf���s���C���̑̐ςƒf�ʂ̕`���Ȑ��Ƒ��ʐςƂ��C�O�p���Ŗʔ����\���ł���Ƃ������Ƃ��܂Ƃ߂�����ł���B �Q�@�����搶�̑Ώ̐��̂�����̒�ϕ��Ƃ�
�@�����搶�̌����ɂ��ƁC�u���ׂĂ̎������ɂ����āC �ł��邩��C�O�q�̂悤�ȁC �@ �@ �@ �@ �@ �@ �@ �@ �@
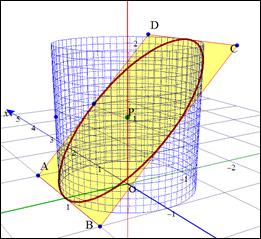
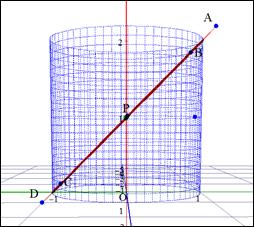
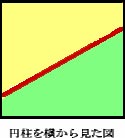
�@����̖��́u�~���̎ߐؒf���f���v�Ƃ������̂́C�E�}�̒ʂ�ł���BGrapes3D���p���āC�����f���ł͂Ȃ��C�}�����̂悤�ɕ\�����B �O��̃��|�[�g�ŁC�~����45���ؒf�Ƃ����C��������]�̂̋��ϖ��ɂ��āC���̃y�[�W�̂悤�Ȗ����l�������C���̗��̂́g�S�̐}�h���l�����悤�Ȃ��̂Ƒz�����Ă���������Ǝv���B �@ �@ �@ �@�{���|�[�g�ł́C�v�Z�̕X��C���a1�̉~�̒�ʂ����C����2�̉~����ؒf���邱�Ƃɂ���B �@ �@ �@ �@ �@ �@ �@ �@
�@(1) �@�̐ςɂ��� �@�̐ςɂ��ẮC������蓙�ł�����݂ł��邽�߁C����͑�����b��ɂ��Ȃ�����ł��邪�C �@�@�f�ʂ� �A�@ �B�@ ���̂悤�ɁC�傫���R�ʂ�̎�@���l�����C���]�̂̋��ϖ��Ƃ��Ă͂��܂�ɂ��L���ł���C�������l����������Ƃ��ċ���I���l�������B �@(2)�@�f�ʂ̕`���Ȑ��ɂ��� �@�f�ʂ͂����̂Ƃ���ȉ~��`���B���̑ȉ~�ł���Ƃ����ؖ����~���ɋ��������Ă���悤�Ȑ}���l����ƊI�ؖ��Ƃ��Ėʔ������C�{���|�[�g�ł͊�������B �\��́u�f�ʂ̕`���Ȑ��v�Ƃ����Ӗ��́C����ʂɓW�J�����Ƃ��̋Ȑ��̕��������Ӗ����Ă���B �~���̕������́C
�ŕ\�����B �}��ϐ��\������ƁC
�ł���B
�@�Ƃ���ŁC�ؒf�ʂ̕��ʂ̕������́C��ʂƃ��̊p�x�Őؒf�����ꍇ�C
�ƂȂ邽�߁C
�ƕ\�����B ��̓I��45���̏ꍇ�́C �@ �@ �@ �@�܂�C�f�ʂ̕`���Ȑ��́C
�ƕ\����邱�Ƃ�������C
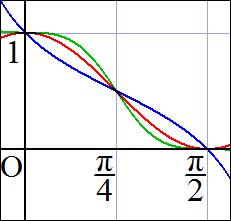
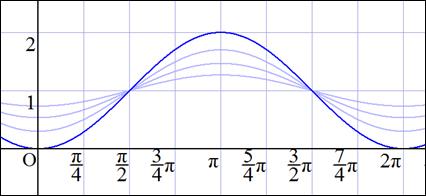
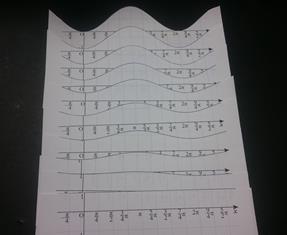
�@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �@ �ł���C���̃O���t�́C���}�̂悤�ɁC����l�X�ɕς���C�܂�߂̐ؒf�p�x��l�X�ɕς��邱�Ƃɂ���āC�T�C���J�[�u�̈���`����Ȃ����Ƃ�������B�i�ł�������45���̏ꍇ�ł���B�j �@�t�ɍl����ƁC���̐����Ȑ����͂��݂Ő���C������ƂP�������C�ŏ��̉~����45���ߐؒf�̗��̂��ł��邱�Ƃ�������B�O�p�����K���n�߂�����̏�Ԃł́C�Ȃ������Ȃ邩�͐�����������C������������ނɂȂ�Ǝv����B �@ �@���ۂɎ�����č���Ă݂����f���͉��̎ʐ^�̂Ƃ���ł���B
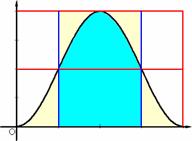
(3)�@���ʐςɂ��� �@���ʐς����߂�v�Z������ƁC��̃O���t�̎R�`�����ʐς����߂�悭�C45���ł́C
�@ �@ �@ �@ �@ �@ �@ �@ �Ƃ��낪����́C���Ƃ̉~���ōl����Ɓi�~���������猩���}���l���āj�C�߂ɓ������������ɉ߂��Ȃ��̂ŁC���ʂ��~���̑��ʂ�^����ɐ蕪���Ă��邱�Ƃ��킩��B����́C�~���̑��ʐς̔����ƍl���Ă悢�B�܂蒷���`�̖ʐς̔����ƍl����悭�C �@ �ł���B �@�����ł悤�₭�C�����搶�́u�_�Ώ̂ȃO���t�̖ʐς́C�S�̂̔����v�̈Ӗ����ǂݎ��邱�ƂɂȂ�B��قǂ́C
�ɂ����āC �@�X�ɁC�����Ȑ��́u�ЂƎR2�v�̗L�������𗘗p���āC �@ �ł��邩��C
�@+�A+�B���l����ƁC
�Ƃ������ϕϊ����C�l����[�߂邽�߂ɂ͖ʔ������낤�B
�@
(4)�@��̓I�Ȏ��ۂɂ��� �~���̐ؒf�̓W�J�}�ȂǁC3������2�����Ƃ��s��������悤�ȍ���̃e�[�}�́C��̓I�Ȃ��̂Ƃ��Đg�̉��ɂ��ӂ�Ă���B���Ƃ̌��ԂŖ��C�o�܂��ɂ��傤�Ǘǂ��̂ł͂Ȃ����낤���B �E���z�ȂǂŌ�����B�����K�i�B �E�����̃T�C���|�[���B �E�m���̑��̕����̓W�J�i�^���j�̋Ȑ��B �E�˂�˂��B
�R�@�܂Ƃ� �@����̂��̃��|�[�g�ł́C���ƒ��Ɋ��p�������H�����ł͂Ȃ��C�����搶�̃��|�[�g�Ƀq���g�āC�l����[�߂Ă����������ł���B���̂��߁C�������������ӂ̘b��k�ɂǂ̂悤�ɊҌ����Ă������C�Ƃ������Ƃ����ɂȂ邾�낤�Ǝv����B�Ⴆ��Ȃ�C�p�C�v�̐ؒf�Ȃǂ̍H�ƓI����Ȃǂ̏�ʂŏ\���Ɍ����I�ȁC���w�������Ă��邱�Ƃ��m�F�ł�����ł͂Ȃ����Ǝv����B �@���̓I�Ȃ��̂́C���k�ɂƂ��ăC���[�W���邱�Ƃ�����悤�ł���B�Q�[���@���X�}�[�g�t�H���Ȃ�2�������ʏ�ŗV�Ԃ��Ƃ��嗬�ɂȂ��Ă��Ă���C���A���ȕ��̂̃p�Y����ςݖ�[�r�b�N�L���[�u�̂悤��3������ԂŁu���́v�ƋY��Ă��Ȃ����Ƃ�����Ƃ��Ă���̂�������Ȃ��B�i�������C�������Ă݂��3D�̃e�g���X�Ȃǂ�����C��T�ɂ͌����Ȃ��悤���B�j �@���w�I�Ȗʔ�����s�v�c����Nj����C�S�苭���l���鐶�k��������Ă����B �@ |
�@