（９６  東京理科大・理）
                                                                 １
１辺の長さが１の正三角形Ｆ１があり、０＜ａ≦----を満たす実数ａが与えられている。
                                                                 ６
正三角形Ｆ１の１つの辺の上に、その辺の中点からａだけ離れた点を２つとる。 
そして、Ｆ１の外側に、この２点を頂点とする正三角形を付け加える。
この操作を、Ｆ１の各辺に行うことによって得られる１２角形をＦ２とする。
次に、１２角形Ｆ２の１つの辺の上に、その辺の中点からｌａだけ離れた点を ２つとる。
ただし、ｌはその辺の長さとする。 そして、Ｆ２の外側に、この２点を頂点とする正三角形を付け加える。
この操作をＦ２の各辺に行うことによって得られる４８角形をＦ３とする。
以下同様に、この操作を繰り返し行うことにより、各自然数ｎについて ３・４n-1角形Ｆｎから、
３・４n角形Ｆｎ＋１をつくることが出来る。 このとき、３・４n-1角形Ｆｎの全ての辺の長さの和をＬｎで表す。
また、Ｆｎのすべての辺の長さの和をＳｎで表す。
          １
　ａ＝----のときのＦ１、Ｆ２、Ｆ３は下図のようになる。
          ６ 　　　　　　　　　　　
             　
(1)Ｌ２とＬ３を求めよ。
(2)Ｌｎを求めよ。
(3)Ｓ２を求めよ。
(4)Ｓｎを求めよ。
(5)３・４n-1角形Ｆｎから３・４n角形Ｆn+1をつくるときに、あらたに付け加えられるすべての正三角形の面積の和はＳｎの何倍か。
(6)３・４n-1角形Ｆｎの面積を求めよ。
－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－
(解)
(1)Ｆ１の１辺は長さ１
                     １ 　
Ｆ２の１辺は（----－ａ＋２ａ）×２＝１＋２ａ
                     ２ 　
これは、１回の操作で、どの辺も(１＋２ａ)倍になることを意味しており、等比数列をなす。
よって、Ｌ１＝３より
 　　　　Ｌ２＝３(１＋２ａ)

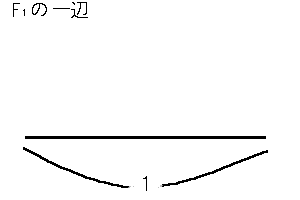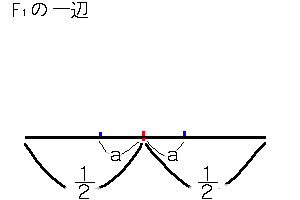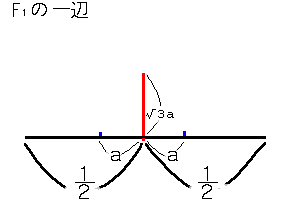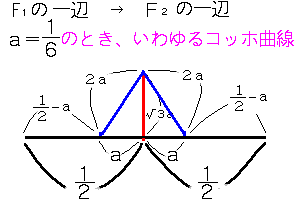
(2)(1)と同様に考えて、Ｌｎ＝３(１＋２ａ)ｎ－１

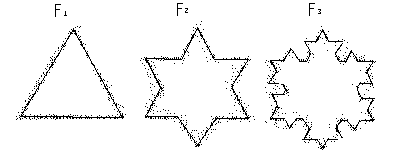
(3)Ｆ１の１辺の長さの２乗の和は、１
                                              １ 　
Ｆ２の１辺の長さの２乗の和は、(----－ａ)２×２＋(２ａ)２×２
                                              ２
                                                                １
                                        ＝１０ａ２－２ａ＋---- …………①
                                                                ２ 　
これは、１回の操作で、どの辺の２乗の和も、①倍になることを意味しており、等比数列をなす。
よって、Ｓ１＝３より
                                         １
　　　　Ｓ２＝３(１０ａ２－２ａ＋----)
                                         ２

(4)(3)と同様に考えて、
                                         １
         Ｓｎ＝３(１０ａ２－２ａ＋----)ｎ－１
                                         ２

(5)長さｌの１辺に対して、新たに付け加えられる面積は、
                              １
　２ａｌ×√３ａｌ×----＝√３ａ２ｌ２
                              ２ 　
これは、ＦｎからＦｎ＋１を作るときの、全ての辺についていえる。
　よって、新たに加える面積の総和は、
　√３ａ２ｌ２のｌ２の部分は、１つの辺についてだから、
　全ての辺については、√３ａ２(ｌ２＋ｌ２＋……) 　つまり、√３ａ２×(すべての辺の長さの２乗の和)であり、
　Ｓｎの√３ａ２倍と言える。

(6)Ｆｎの面積をＴｎをおく。ｎ≧２のとき、
　Ｔｎ＝Ｔ１＋√３ａ２Ｓ１＋√３ａ２Ｓ２＋…………＋√３ａ２Ｓｎ－１
            √３
　　　＝----＋√３ａ２（Ｓ１ ＋Ｓ２＋…………＋Ｓｎ－１）
             ４
           √３             n-1                         １    ｋ－１
 　　 ＝----＋√３ａ２Σ ３（１０ａ２－２ａ＋----）
            ４               k=1                         ２
             １                                  １
０＜ａ≦----のとき、１０ａ２－２ａ＋----≠１より
             ６                                  ２
　　                                                            １    ｎ－１
                                    １－（１０ａ２－２ａ＋----）
         √３ 　　 　　                                       ２
　　 ＝----＋３√３ａ２   -------------------------
           ４                                           　 　　 １
                                    １－（１０ａ２－２ａ＋----）
　　                                                            ２
　　　である。これは、ｎ＝１のときも成り立つ。